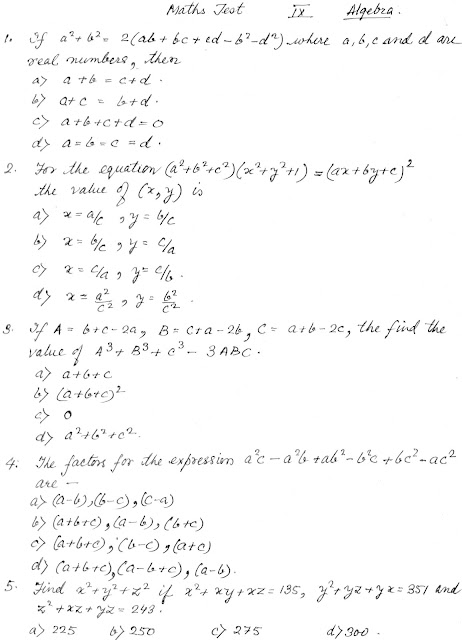Algebra test - STD VIII and STD IX

Factors

numbers

How many 4 digit nos.are there that is divisible by 29 and the sum of digits are equal to 29.

IPM/MTSE/JMO practice papers

IPM/MTSE/JMO practice papers

Puzzle

There are a 1000 locks in closed position. 1000 children numbering 1 to 1000 approach the lock one by one. The rule is the child (say with number 'n') can open or close the lock numbering  in multiples of "n" only.
so the child in number one position can open all the locks. Child number 2 will be able to close all the locks in multiples of 2 (like 2, 4, 6 .... upto 1000). The other locks will remain as they are.
After all the 1000 children have had their chance, how many locks will be in open position.

geometry

 
















I would appreciate receiving your solutions.

geometry - triangle

A triangle has a perimeter of 36 cm. The altitudes of the triangles are in the ratio of 1:2:3. Find the measure of each sides.

Teaser on area

ABCD is a rectangle. The area of shaded region is 15 cm2. find the area of rectangle ABCD

Another Teaser on Area

Find the Area of rectangle ABCD
given area of triangle AOC = 40 m2
and area of triangle BOD = 30% of area of Rectangle ABCD

Teaser on Area

Find the Area of rectangle ABCD
given area of triangle AOC = 60 m2
and area of triangle AOB = 40% of area of Rectangle ABCD

scratch your brains guys....this is interesting

Nanu's Grandfather's age is a 2 digit number and her father's age is reverse of her grandfather's age. Nanu's age is 4 times the difference in age between her grandfather and her father. What is Nanu's age.

answer 9 years

Coordinate Geometry - Singapore Maths Olympiad

Let A and B be points that lie on the parabola y = x² such that both are at a distance of 8√2 units from the line y = -x – 4. Find the square of distance between A and B

Geometry

Given an equilateral triangle, what is the ratio of the area of circumscribed circle to the are of its inscribed circle?

Sets and Relations - Singapore Maths Olympiad

Suppose that a function M(n), where n is a +ve integer, is defined by
M(n) = n - 10 for n > 100
M(n) = M(M(n +11) for n ≤ 100
How many solutions does the equation M(n) = 91 have?

Singapore maths Olympiad

Let a,b,c,d be real numbers such that a² + b² + 2a – 4b + 4 = 0 and c² + d² – 4c + 4d + 4 = 0.

Let m and M be minimum and Maximum value of (a – c)² + (b – d)² respectively. What is m x M.

Singapore maths olympiad, number

If a₁, a₂, a₃, .............. a₂₀₁₁ are positive integers such that (a₁ + a₂ + .....a₂₀₁₁) = a₁.a₂.....a₂₀₁₁

Then find the max value of (a₁ + a₂ + .....a₂₀₁₁)

Singapore maths Olympiad

Find the largest positive integer ‘n’ such that (n + 10) is a divisor of n³ + 2011

Singapore maths Olympiad, Numbers

Let 'n' be the smallest positive integer such that the sum of its digits is 2011. how many digits does 'n' have?

Probability, Singapore Maths Olympiad

A fair dice is thrown 3 times. the results of the first, second and the third throw are recorded as x, y and z respectively. Suppose x + y = z. What is the probability that one of x,y,z is atleast 2?

Singapore Maths Olympiad

Singapore Maths Olympiad